NOSIGNER - Pattern / Evolutional Creativity

why:

Increase the number of innovators learning from the creativity of biological evolution.

創造性を生物の進化から学び変革者を増やす。

Society is changing drastically. Even now 50 years later since 1972, which was said to be the limit of growth for human beings, we are still growing today. Changes to halt the collapse of biodiversity and actions to keep a sustainable society no longer have a temporal grace. We need more people to change society. We often say that things "evolve" changing society. If we say that the changing society is evolving, will we be able to learn more about the process of this evolving society, from the evolution of living things?

社会は急激に変わっています。成長の限界と言われた1972年から50年が経った今でも、我々人類はまだ成長し続けています。生物多様性の崩壊を食い止めるための変化や持続可能な社会を保つためのアクションは、もう時間的な猶予が全く残されていない状況と言っていいでしょう。社会を変える人がもっとたくさん必要だと、心から感じます。どうすれば、そのような人を増やせるのでしょうか。そういえば私達は、物が社会を変えることを「進化する」とよく言っています。社会を変えることが進化だと言うなら、私達はもっと生物の進化から社会の進化を生むためのプロセスを学ぶことができるのではないでしょうか。

Horizontal, vertical and gravity.

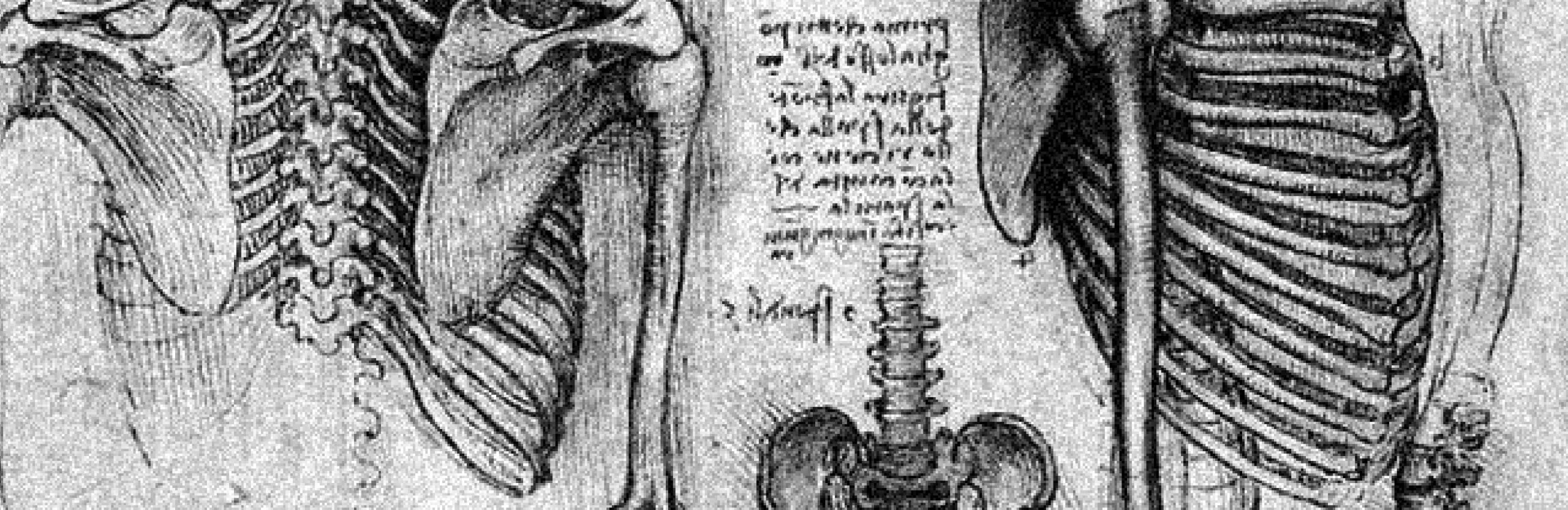
When creating forms, humans often make use of quadrilateral and cubic shapes, but regular quadrilaterals are almost never found in the natural world. With the exception of a small number of crystalline structures such as pyrites and bismuth crystals, nature has chosen triangular forms over quadrilateral ones. The reason for this is easy to understand when we see that a tetrahedron (in which all surfaces are equilateral triangles) offers a far stronger structure than that of a cube (in which all surfaces are square). The quadrilateral structures that humans have chosen as the standard for their buildings are, in fact, quite unstable. So, when can we find horizontal and vertical lines in nature? The answer is in lines created by gravity. If you put a weight on the end of a thread and let it drop down, it will form a flawless vertical line. The horizon on the sea is an almost-perfect horizontal line. In this way, nature achieves verticality by counteracting gravity, and horizontality when it is defeated by that gravity. Humans, owing to the fact that their bodies are bound by the force of gravity, have also evolved in adaptation to the horizontal and the vertical. Our field of vision is effective for surveying our surrounds horizontally. It is surely because our eyes are optimized to move horizontally that most part of the world developed horizontal writing systems. This is probably evidence of the extent to which culture is influenced by gravity.

Symmetry and stability.

Things that are symmetrical are stable. Considering the balance between the forces that work internally such as stress and gravity, it is possible to see symmetry as an inevitable choice in most environments. Symmetry can be observed in all forms of life. The fewr limitation there are, the closer forms get to pure symmetry. In entities small enough for gravity to be irrelevant, such as pollen, or viruses, there are numerous exquisite geometric forms based on polyhedral structures and spherical shapes with three-dimensional symmetry with respect to both point and plane. Larger organisms are subject to more restrictions, so it becomes more difficult to preserve symmetry; nonetheless, nature seeks to do so, and evolution takes the direction of two-dimensional point or plane symmetry (such as in flowers and snow), or line symmetry (in animals, leaves, and so on). Ultimately, even in the case of large animals such as elephants, most solid organisms have evolved while preserving bodily linear symmetry. Nature seeks to maintain symmetry wherever possible for the purpose of stability. Seeing beauty in the strong symmetry of flowers is not something unique to humans; it is a universal reaction common to all living creatures, including the insects that flowers attract. Living creatures seek symmetry instinctively.

水平垂直と重力。

人は造形によく四角形や立方体を用いるが、自然界にはほとんど正四角形は存在しない。パイライトやビスマス結晶のような、ごく一部の結晶構造を除いて、自然は四角形よりも三角形を選んできた。その理由は、立方体（すべての面が正方形）と正四面体（すべての面が正三角形）を比べてみると、圧倒的に正四面体の構造のほうが強いことからもよく分かる。人間が建築の標準的な構造に選んでいる四角形は、実はたいへん不安定なものなのだ。では、水平と垂直の線が自然界に現れるのはいつだろうか。それは重力によって生まれる線だ。糸の先に重りをつけて垂らすと、完璧な垂直線が得られる。あるいは海の水平線は、ほぼ完全な平行線を描く。このように自然は, 重力と拮抗することで垂直性を手に入れ、逆に重力に負ける形で水平性を得る。人間もまた、重力に縛られた身体を持つが故に、水平と垂直に最適化して進化した。人の視界は平行に周囲を見まわすために効率よくできている。世界の文字の中で、横書きの文字が発達した地域が多いのは、水平に動く目に最適化されているからだろう。その事実は、文化に対する重力の影響がいかに大きいかを表しているように思う。

対称性と安定。

対称形を持つものは安定する。内部に働く応力や重力とのバランスを考えると、対称形は多くの環境において必然的な選択と言えるだろう。対称形はあらゆる生物に見られる。そして、制約がなければないほどに、対称的な形に近づいていく。花粉やウィルスなど、微小で重力の影響を受けない物体においては、3次元的に点対称となる球体型や多面体構造を基本とした、美しい幾何学的な造形が数多く存在する。それよりも少し大きな自然物の場合、周囲からの制約が増えるために対称性を維持するのが困難になるが、それでも自然は対称を維持しようとして、点対称や面対称（雪や花など）あるいは線対称（動物や葉など）の方向に進化する。最終的にはゾウのように大きな生物であっても、ほとんどの個体は身体に対称性を維持して進化している。自然は安定のために可能な限り対称性を維持しようとする性質があるのだ。強い対称性を持った花を美しいと感じるのは、私達人間だけでなく、引き寄せられる虫など全ての生物に共通の感覚なのかもしれない。

how:

Essential forms hold common patterns.

本質的な形態には、共通のパターンがある。

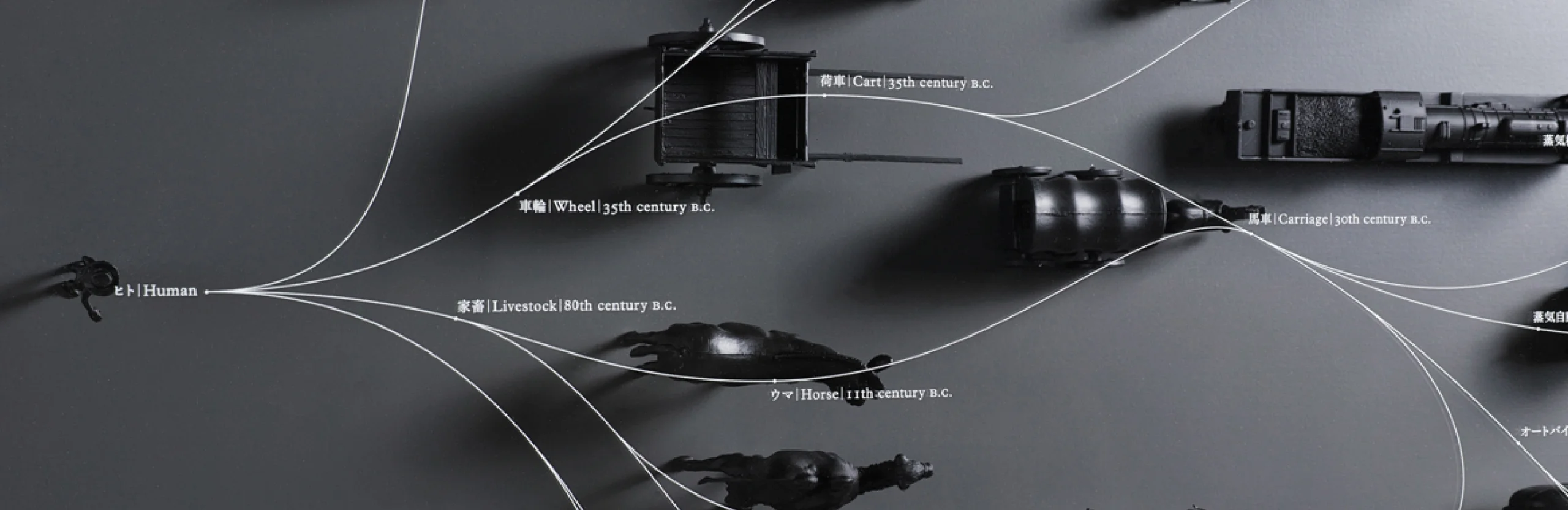
Even in the design of artifacts, things are constantly evolving and culling from advances in technology, human interests and within the changing context of time. The development of species on the premise of diversity closely resembles the form of evolution of living things. The invention constantly seeks to supplement the evolution of people. Being faster and more comfortable is perhaps not the kind of design that has been advanced by such philosophy and instinct of mankind. If evolution and the design of living organisms are sufficiently similar, it should make innovation easier, by understanding the process well, applying this to inventions and designs. "Evolution Thinking" is a methodology of creativity for education, to learn the ways of thinking, from nature.

人工物のデザインにおいても, 技術の進歩, 人の趣向性や時代のコンテクストの変容によって, モノは絶えず進化と淘汰を繰り返しています。多様性を前提とした種の発達は, 生物の進化の形によく似ています。常に発明は人の進化を補おうとしているようにも感じられます。より速く, より楽に、そんな哲学によって進められてきたデザインは, 進化しようとする人類の本能ではないでしょうか。もし生物の進化とデザインが充分に似ているなら、そのプロセスをよく理解し、発明やデザインに応用することでイノベーションを起こしやすくなるはず。進化思考は、そのような考え方から生まれた、自然から学ぶ新しい創造教育のための手法です。

Voronoi diagrams and harmony.

In nature, there is a tendency to minimize elements and seek harmony. Bubbles, for example, shrink to the smallest surface area necessary in order to contain the air inside them. In this process, they interlock with the bubbles adjacent to them and create beautiful geometric patterns with polygons. Similar geometric patterns appear in a wide range of contexts in the natural world, including beehives, cicadas’ wings, giraffes’ stripes, and the rocks of the Giant’s Causeway in the UK. Such patterns can be explained using a simple mathematical model known as a Voronoi diagram. Used where a set of points interact in close proximity Voronoi diagrams are created by following simple rules of geometry to draw intermediary lines between the points and thereby creating boundaries around them. The result could be said to be the type of shape that nature draws automatically in cases where numerous points coexist in virtual equivalence to one another. It is surely no coincidence that we find beauty in forms that approach an optimal state. If we could create a building with an ideal level of mobility, it would surely be one in which, as soon as an adjacent room becomes vacant, walls move automatically, leaving only the space necessary to fulfil the building’s functions with minimal use of materials. If it were possible to achieve such an ideal building, it may well have a layout similar to a Voronoi diagram.

Turing patterns and ambiguity.

In the natural world, there are many patterns with imperfect regularity, such as a zebra’s stripes, or sand dunes in a desert. Sometimes, remarkably similar patterns can be observed across entirely different phenomena. The fundamental law of these repeating patterns was revealed by the brilliant mathematician Alan Turing, who also formulated the basic concept of modern computing. In the final years before his untimely death at a young age, Turing discovered that natural striped patterns are created through convective flows occurring between multiple elements. The patterns have been known as “Turing patterns” ever since. Two or more mobile elements with different densities that intermingle produce convection, which becomes fluctuation, creating patterns. In fact, a Voronoi diagram is a type of Turing pattern generated under special conditions where there are multiple equivalent centers. The beauty that we sense in patterns generated by convection is close to the feeling of comfort derived from the rhythms we perceive in variations between perfection and imperfection. Turing patterns could be said to be nature’s manifestation of musical form.

チューリングパターンと両義性。

シマウマの柄や砂漠の砂丘など, 自然界には不完全な規則性のある模様が数多く存在する。全く違う現象の間にも, 本当に良く似た模様が観察されることがあるが, その基本法則を明らかにしたのはコンピューターの基本概念を作った天才数学者アラン・チューリングだった。彼は若くして亡くなるその晩年に, これらの自然の模様が複数の要素の間に働く対流によって生まれることを発見した。それ以来, この縞模様はチューリングパターンと呼ばれている。流動性があり密度の異なる要素が複数ある場合に, その両方が絡み合おうとすると対流が生まれ, それがゆらぎとなって, 模様をつくりだすのだ。実はボロノイ図も, 複数の中心が等価にあるような特別なコンディションにおいて生まれてくるチューリングパターンの一種である。対流が生み出すパターンを美しいと思う感覚というのは, 完全と不完全の間にあるゆらぎにリズムを見出し, そのリズムを心地良いと思う感覚に近い。チューリングパターンは, 自然が見せる音楽的な造形と言えるかもしれない。

ボロノイと調和。

自然には, 要素を最小化して調和を指向する性質がある。例えば泡は, 内部の空気を閉じ込めておける最小の表面積まで縮もうとする。その過程で, 隣の泡とせめぎ合いながら, 多角形の美しい幾何学模様を描く。泡と同じような幾何学模様は, 蜂の巣, セミの羽, キリンの縞, イギリスのジャイアンツ・コーズウェー海岸の岩など, 自然界の様々なところに現れるが, このパターンはボロノイ図(Voronoi)と呼ばれる。ボロノイ図は, たくさんの点がせめぎあう状態で, 点と点の間に境界となる中間の線を引いていく, という単純なルールの幾何学だ。多くの点がほとんど等価値で共存する場合に, 自然が自動的に描く形と言えるだろう。最適化を目指す形を, 僕らが美しいと感じるのはきっと偶然ではない。もし理想的な流動性を持つビルができるなら, 隣の部屋が空いた途端に壁が自動的に動き, 最小限の部材で空室分の空間が拡張されるはずだ。もし, そんな建物が実現したら, それはボロノイ図のような間取りを持っているかもしれない。

No matter how much you enlarge a map of a jagged coastline, it will always remain complex. The length of such a coastline cannot be measured accurately. Figures that retain the same pattern no matter how much they are enlarged are known as fractals (self-similar forms). Almost all natural objects produce some type of self-similarity as they grow, and thus end up with forms that create fractals. Fractals are also closely connected with the forms that humans perceive as beautiful. A handsome forked tree branch and the complex diverging flickers of a sparkling firework are two of the many examples of fractals. It is interesting to note that the network of the internet also has a fractal structure almost identical to that of a sparkling firework. As the network grew naturally, it must have developed self-similarity. Fireworks are the greatest visual installation created by humankind, and the internet is one of the most successful inventions in human history; the fact that they both possess the fractal property of self-similarity is truly fascinating. Perhaps we are now seeking to uncover a new type of fractal form through invention.

Fibonacci and growth.

In Liber Abaci written in 1202, Leonardo Fibonacci presented a numerical sequence (known as Fibonacci numbers) to calculate how fast a single rabbit would produce four rabbits if it mated and reproduced regularly. Fibonacci is said to have learned this fascinating sequence while he was studying in India. Later developments in the natural sciences and morphology revealed the deep relationships between Fibonacci’s simple rule and patterns of growth in the natural world. Take, for example, the growth of a tree. The point at which a branch will diverge, the kind of spiral shape that will be created by growing foliage when viewed from directly above, the speed at which the foliage will increase in size—all these things are governed by the Fibonacci sequence. The breadth of application for this theory of forms in the natural world is astounding. The golden ratio (1:1.618), said to be the most aesthetically pleasing ratio for humans, is also derived from Fibonacci numbers. The instinct for beauty running through life itself recognizes forms that continue their growth unceasingly while retaining their symmetry. Here we catch a fleeting glimpse of the instinctive will to grow.

複雑な海岸線を地図上でどこまで拡大していっても, 最後まで複雑な線であることは変わらない。だから海岸線の正確な長さを測ることはできない。このように, どんなに拡大しても, 同じようなパターンを持つ図形をフラクタル（自己相似形）という。ほとんどの自然物は, 成長する時に何らかの自己相似形を生み出すため, 結果的にフラクタルを成す形をつくる。人が美しいと思う造形もまた, フラクタルと密接に関わっている。枝ぶりの美しい分岐や, 幾重にも分岐する雷もまた, フラクタルの一例だ。興味深いことに, インターネットのネットワークの形や線香花火もフラクタル構造を持っている。ネットワークが自然に成長する過程で, 自己相似形を成してしまったのだろう。花火は人類が生み出した最高のインスタレーションであり, インターネットは人間の歴史において最も成功した発明の一つだが, それらがフラクタルの相似形をしているというのは, とても興味深い事実だ。僕たちは発明を通して次のフラクタル図形を探しているのかもしれない。

フィボナッチと成長。

レオナルド・フィボナッチは西暦1202年に「算盤の書」の中で, ウサギが定期的に出産をし, 交配を続けると何匹になるかを計算する数列（フィボナッチ数）を発表した。フィボナッチがインドに留学している間に, 現地で学んできたという不思議な数列だ。その後の自然科学と形態学の発展は, この単純な法則と自然物の成長パターンの間に, 密接な関係があることを明らかにした。木の若葉の成長を例に取れば, 枝がどのような位置で分岐していくか, 真上から見た時に葉の生える位置がどう螺旋を描くか, そして葉がどのようなスピードで大きくなっていくのかもまた, このフィボナッチの数列に支配されているというのだから, この比率でカバーされる自然の造形論理の範囲は驚くほど広い。人が最も美しいと感じると言われている黄金比（約1:1.618）もまた, このフィボナッチ数によって導かれるものだ。対称性を保ちながら, とどまることなく成長を続ける造形を, 生命に流れる美の本能は感じとる。そこに自然が持っている, 本能的な成長への意志が見え隠れする。

will:

Evolution Thinking came to be by integrating all ways of thinking.

あらゆる発想法を統合する進化思考の誕生。

The evolutionary thought that started with a small experimental exhibition is gradually spreading while being gradually supported by "Evolution Thinking" started as a small experimental exhibition, and is currently gradually spreading, while being supported by proponents such as the automobile company, the real estate company of the largest scale in Japan and the manager of the global company of apparel. (Reference article: Harvard Business review etc). We will continue to provide "Evolution Thinking" as a program to nurture innovators that change society. In order to realize a sustainable symbiotic society, do not you think that there is at least one innovator within 2000 people, aiming for social change? While it is said that by 2050 the population will exceed 10 billion, one in 2000 is one in five million. With that, we believe that a superior educational program that truly brings up a number of people who realize social change is necessary.

小さな実験的展示から始まった進化思考は、いま日本最大級の規模の自動車会社・不動産会社やアパレルのグローバル企業の経営者など、徐々に賛同者に応援されながら広がりつつあります。（参考記事：Harvard Business review etc）私たちは進化思考を社会を変えるイノベーターを育てるためのプログラムとして提供し続けます。持続可能な共生社会の実現のためには、最低でも2000人に1人程度は、社会変革を目指すイノベーターがいてもいいと思いませんか。2050年までには人口が100億を突破すると言われている中で、2000人に1人は500万人。そのためには、本当に社会変革を実現する人を数多く育てる優れた教育プログラムが’必要だと考えています。

what:

Pattern / Evolutional Creativity

when:

2016

where:

Ginza, Tokyo, Japan

who:

Art Direction

NOSIGNER (Eisuke Tachikawa)
Graphic Design

NOSIGNER (Eisuke Tachikawa, Toshiyuki Nakaie)
Space Design

NOSIGNER (Eisuke Tachikawa, Sui Fujikawa)

Photo